Módulo 1: Análisis de inversiones
U.D. 3: Obligaciones y bonos. Empréstitos.
Sección: 2
MathJax TeX Test Page
3.02
EMPRÉSTITOS
3.02.01
Concepto
Un empréstito es una emisión de obligaciones y constituye
una de las formas de financiación para la empresa, si bien es verdad,
que su uso se reserva para las grandes empresas, fundamentalmente motivado
por la confianza que el inversor tiene en ellas.
3.02.02
Tipos de empréstitos
Para darnos una idea genérica de los tipos de empréstitos,
veamos el siguiente diagrama:
Empréstitos |
Sin cancelación escalonada
(sin sorteos) |
Con cancelación escalonada
(con sorteos) |
Formados por obligaciones de tipo americano |
|
Formados por obligaciones que representan préstamos simples |
|
Formados por obligaciones de tipo americano |
|
Formados por obligaciones que representan préstamos simples |
|
Interés constante
Interés variable |
|
Interés constante
Interés variable
Términos amortizativos constantes o variables |
|
Interés constante
Interés variable
Términos amortizativos constantes o variables |
|
Interés constante
Interés variable
Términos amortizativos constantes o variables |
|
Todas ellas, pueden incluir una serie de características comerciales
como son: primas de reembolso, lotes y primas de emisión.
En este tratado se estudiarán los empréstitos con cancelación
escalonada, es decir, con sorteos periódicos de amortización
de títulos, con tipo de interés constante a lo largo de
la vida del empréstito y términos amortizativos constantes,
haciendo una breve referencia al caso anterior, pero con términos
amortizativos variables. No es nuestro objetivo el estudio en profundidad
de los empréstitos. No obstante, con los conocimientos adquiridos
en esta unidad, estaríamos en predisposición para poder
entender el resto de tipos de empréstitos.
3.02.03
Empréstitos
formados por obligaciones tipo americano con cancelación escalonada
3.02.03.01
Planteamiento
general
Se trata de empréstitos formados por obligaciones de tipo americano
y con realización de sorteos periódicos, en los cuales se
amortizan un determinado número de títulos.
Las variables que intervienen en el planteamiento son:
-
Ns
:
número de títulos pendientes
de amortizar al inicio del período "s".
-
Ms
:
número de títulos amortizados
al final del período "s".
-
as
:
término amortizativo o cantidad pagada
a los obligacionistas al final del período "s".
-
is
:
tipo de interés en el período
"s".
-
Cs
:
capital pendiente de devolver a los obligacionistas
al final del período "s", una vez pagado el término
amortizativo as.
-
Vo
:
valor nominal de la obligación.
El planteamiento es que al final de cada período se pagan los intereses
del mismo a todas las obligaciones vivas al inicio de dicho período
y se amortizan un número determinado de ellas, es decir se reembolsa
a los obligacionistas el nominal de dichos títulos amortizados.
Las obligaciones amortizadas se obtienen mediante sorteo en la forma expuesta
en el artículo 308 de la Ley de Sociedades Anónimas expuesto
en el apartado 3.01.01.
Esquemáticamente podríamos representarlo así:

$$Intereses \ldots
V_{0}
\centerdot N_{1}
\centerdot i_{1\ldots\ldots\ldots }
V_{0}
\centerdot N_{2}
\centerdot i_{2}
\ldots\ldots\ldots
V_{0}
\centerdot N_{n}
\centerdot i_{n}$$
+
$$amortización\ldots M_{1}
\centerdot V_{0}
\ldots\ldots\ldots M_{2}
\centerdot V_{0}
\ldots\ldots\ldots M_{m}
\centerdot V_{0}
$$
$$términos\ amortizativos\underset{a1}{
{V_{0}\centerdot N_{1}\centerdot i_{1}+M_{1}\centerdot V_{0}}}\ldots\ldots\ldots\ldots\underset{a2}{ V_{0}\centerdot N_{2}\centerdot i_{2}+M_{2}
\centerdot V_{0}}
\ldots\ldots\ldots\ldots\underset{an}{ V_{0}\centerdot N_{n}\centerdot i_{n}M_{m}
\centerdot V_{0}}$$
Es evidente que el número de obligaciones
vivas al inicio del segundo período, serán las que
eran vivas al final del primer período menos la que hayamos amortizado,
es decir, se verificará:
N1
M1 = N2
_______________________
N1
N2 = M1
y en general:
Ns
Ns+1 = Ms
También es evidente que la suma de todas las obligaciones amortizadas,
deberá coincidir con el número de obligaciones vivas al
inicio del empréstito, por tanto, se verificará:
M1
+ M2 + ........... + Mn
= N1
o bien en forma condensada:
$$\underset{s=1}{\overset{n}{\sum}}
M_{s}
=N_{1}$$
Observemos que en el planteamiento general, los tipos de interés
de los períodos o réditos periodales y los términos
amortizativos, son variables a lo largo de la vida del empréstito.
El planteamiento general de los conceptos básicos nos conduce a
las siguientes expresiones:
A)
Equivalencia financiera en el origen (to):
$$V_{0}
\centerdot N_{1}
=\frac{a_{1}}{\left(1+i_{1}\right)}
+\frac{a_{2}}{\left(1+i_{1}\right)\centerdot\left(1+i_{2}\right)}
+\ldots\ldots+\frac{a_{n}}{\left(1+i_{1}\right)\centerdot\ldots\ldots\centerdot\left(1+i_{n}\right)}
=$$
$$a_{1}
\centerdot\left(1+i_{1}\right)
^{-1}
+a_{2}
\centerdot
\left(1+i_{1}\right)
^{-1}
\centerdot
\left(1+i_{2}\right)
^{-1}
+\ldots\ldots+a_{n}
\centerdot\left(1+i_{1}\right)
^{-1}
\centerdot\ldots\ldots\centerdot\left(1+i_{n}\right)
^{-1}
$$
$$=\underset{s=1}{\overset{n}{\sum}}a_{s}\centerdot\underset{r=1}{\overset{s}{\prod}}
\left(1+i_{r}\right)
^{-1}$$
Es decir, que el montante del empréstito en el origen, debe
ser igual a la actualización en el origen de todos los términos
amortizativos.
B)
El capital pendiente de devolver a los obligacionistas
al final del período "s", una vez pagado el término
amortizativo "as", conocido como reserva matemática,
es:
$$C_{s}
=\frac{a_{s}+1}{\left(1+i_{s+1}\right)}
+\frac{a_{s}+2}{\left(1+i_{s+1}\right)\centerdot\left(1+i_{s+2}\right)}
+\ldots\ldots+\frac{a_{n}}{\left(1+i_{s+1}\right)\centerdot\ldots\ldots\centerdot\left(1+i_{n}\right)}
=$$
$$=a_{s+1}
\centerdot
\left(1+i_{s+1}\right)
^{-1}
+a_{s+2}
\centerdot\left(1+i_{s+1}\right)
^{-1}
\centerdot
\left(1+i_{s+2}\right)
^{-1}
+\ldots\ldots+$$
$$=a_{n}
\centerdot
\left(1+i_{s+1}\right)
^{-1}
\centerdot\ldots\ldots\centerdot\left(1+i_{n}\right)
^{-1}
=$$
$$=\underset{r=s+1}{\overset{n}{\sum}}a_{r}\centerdot\underset{j=s+1}{\overset{r}{\prod}}
\left(1+i_{j}\right)
^{-1}$$
Como vemos, el capital pendiente de devolución al final del
período "s", una vez pagado el término amortizativo
"as", es la actualización al final del período
"s" del resto de términos amortizativos hasta el
final de la vida del empréstito.
C)
Término amortizativo:
$$a_{s}
=\underbrace{V_{0}\centerdot N_{s}\centerdot i_{s}}
+\underbrace{M_{s}\centerdot V_{0}}$$
intereses del período "s" / obligaciones amortizadas del período"s"
3.02.03.02
Caso de réditos
periodales constantes y términos amortizativos constantes
En este caso se verificará:
1)
i1
=
i2
=
i3
=
.....
=
in
=
i
2)
a1
=
a2
=
a3
=
.....
=
an
=
a
Las expresiones de la equivalencia financiera, reserva matemática
y término amortizativo serán:
A)
Equivalencia financiera en el origen:
$$V_{0}\centerdot N_{1}
=\frac{a}{1+i}
+\frac{a}{\left(1+i\right)^{2}}
+\ldots\ldots+\frac{a}{\left(1+i\right)^{n}}=$$
$$=a\centerdot\left[\frac{1}{1+i}+\frac{1}{^{^{\left(1+i\right)^{2}}}}+\ldots\ldots+\frac{1}{\left(1+i\right)^{n}}\right]
=$$
$$a\centerdot\left[\frac{1-\frac{1}{\left(1+i\right){}^{\left(n-s\right)}}}{i}\right]
=a\centerdot a
_{n}\neg
_{i}$$
De donde se deduce la cuantía del término amortizativo,
a, puesto que Vo, N1,
i, son conocidos. Su expresión será:
$$a= \frac{V_{0\centerdot}N_{1}}{a_{n\urcorner i}}$$
NOTA: La suma del corchete
es una serie geométrica análoga a la vista
en el apartado 2.02.02.01, correspondiente a la amortización
de préstamos por el método francés.
B)
Reserva matemática:
$$C_{s}
=\frac{a}{1+i}
+\frac{a}{\left(1+i\right)^{2}}
+\ldots\ldots+\frac{a}{\left(1+i\right)^{n-s}}
=a\centerdot\left[\frac{1}{1+i}+\frac{1}{^{^{\left(1+i\right)^{2}}}}+\ldots\ldots+\frac{1}{\left(1+i\right)^{n-s}}\right]
=$$
$$a\centerdot\left[\frac{1-\frac{1}{\left(1+i\right){}^{\left(n-s\right)}}}{i}\right]
=a\centerdot a
_{n-s}\neg
_{i}$$
$$= \frac{V_{0\centerdot}N_{1}}{a}\centerdot
a_{n-s\urcorner i}
$$
NOTA: La suma del corchete
es una serie geométrica análoga a la obtenida
al estudiar la equivalencia financiera, pero con "(n-s)"
en lugar de "n".
C)
Término amortizativo:
$$a_{s}
=a=\frac{V_{0\centerdot}\centerdot N_{1}}{an\urcorner i}
para\ s=1,2,\ldots\ldots,n$$
De la constancia del término amortizativo, podemos hallar
el número de obligaciones a amortizar al final de cada período,
con sólo restar estas dos expresiones miembro a miembro:
$$a_{s}=a=V_{0}N_{s}\centerdot i+V_{0}.M_{s}$$
(-)
$$a_{s+1}=a=V_{0}N_{s}\centerdot i+V_{0}.M_{s+1}$$
$$0=V_{0}
\centerdot i\centerdot\left(\underset{M_{S}}{N_{s}-N_{s+1}}\right)
+V_{0}
\centerdot M_{s}
-V_{0\centerdot}
M_{s+1}$$
Vo.Ms+1=Vo.Ms .(1+i)
$$M_{s+1}
=M_{s}
\centerdot
\left(1+i\right)
\Longrightarrow
M_{s+1}
=M_{1}
\centerdot
\left(1+i\right)$$
De forma que el número de obligaciones amortizadas al final
de cada período, sigue una serie geométrica de razón
"(1 + i)" y cuyo primer término, "M1",
lo obtendríamos de la expresión del término
amortizativo para el primer período:
$$a=V
_{0}
\centerdot N_{1}
\centerdot i+
V
_{0}
\centerdot M_{1}$$
$$\frac{V_{0}\centerdot N_{1}}{a\ n\urcorner i}
=V
_{0}
\centerdot N_{1}
\centerdot i+
V
_{0}
\centerdot M_{1}
$$
$$M_{1}
=\frac{N_{1}}{an\urcorner i}
=N_{1}
\centerdot i
=N_{1}
\centerdot
\left[\frac{1}{an\urcorner i}-1\right]
=\frac{N_{1}}{S_{n}\urcorner}$$
De esta forma, podremos saber cuantas obligaciones debemos amortizar
al final de cada período, el número de obligaciones
vivas, el montante de intereses a pagar y el término amortizativo,
en definitiva, todo lo necesario para poder construir el cuadro
de amortización del empréstito.
NOTA:
$$\frac{1}{an\urcorner i}-1
=\frac{1}{S_{n}\urcorner i}$$esta igualdad se deduce fácilmente:
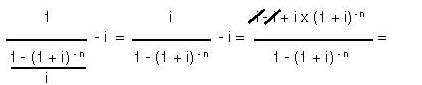
$$=\frac{i}{\left(1+i\right)^{n}-1}
=\frac{1}{\frac{\left(1+i\right)^{n}-1}{i}}=\frac{1}{S_{n}\urcorner i}$$
$$Donde{S_{n}\urcorner i}\ sería\ la\ suma\ de\ la\ serie\ geométrica: 1+(1+i)+(1+i)^{2}+..........+(1+i)^{n-1}$$
Esto es lógico, si pensamos que el número de obligaciones vivas al inicio del empréstito, es la suma de todas las que amortizaremos y éstas siguen una serie geométrica, como ya hemos visto, y por tanto el número de obligaciones vivas al inicio del empréstito será una suma de una serie geométrica:
$$N_{1}
=\overset{n}{\underset{s=1}{\sum}}
M_{s}
=\overset{n}{\underset{s=1}{\sum}}
M_{1}
\left(1+i\right)
^{^{s-1}}
=M_{1}
\overset{n}{\underset{s=1}{\sum}}
\left(1+i\right)
^{s-1}
=$$$$=M_{1}
\centerdot\left[1+\left(1+i\right)+\left(1+i\right)^{2}+\ldots\ldots+\left(1+i\right)^{n-1}\right]
=$$
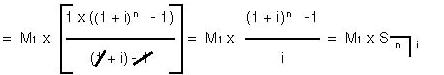
La variabilidad de los términos amortizativos puede obedecer a
determinadas leyes, como por ejemplo, que los términos amortizativos
varíen siguiendo una serie geométrica, una serie aritmética,
etc. El cálculo de los términos amortizativos en cualquiera
de las variaciones mencionadas, es de una complejidad que excede al nivel
de este tratado y por tanto no serán desarrollados, no obstante,
se mencionan para que el lector se dé cuenta de las muchas posibilidades
que la unidad de los empréstitos ofrece en cuanto a cálculo.
Remitimos al lector a un buen tratado de matemática financiera
para abarcar las principales modalidades que ofrecen las variaciones de
los términos amortizativos.