Módulo 1: Análisis de inversiones
U.D. 3: Obligaciones y bonos. Empréstitos.
Sección: 1

3.01 OBLIGACIONES Y BONOS

3.01.01 Concepto

Las obligaciones y los bonos son títulos que representan una parte alícuota de una deuda, que el emisor de dicho título se compromete a pagar al tenedor en un plazo y con unos intereses pactados.

La diferencia entre obligaciones y bonos estriba, fundamentalmente en el plazo de vencimiento, que en las obligaciones es más largo, y en el sistema de amortización. En general, los bonos suelen tener un único vencimiento, mientras que las obligaciones pueden amortizarse anticipadamente a su vencimiento mediante sorteos.

La obligación, en su estado más puro, representa que por dicho título recibiremos unos intereses, en unos plazos determinados, y que al vencimiento nos reintegrarán el nominal del título, es decir, el valor por el que fue adquirido. No obstante, frente a la fuerte competencia que ofrece el mercado de renta variable ante la decisión de un inversor a colocar dinero en dicho mercado o en renta fija, las obligaciones han ido adoptando ciertas formas que la apartan de su concepto primitivo, con el fin de hacerlas más atractivas frente al inversor, es por ello que en la actualidad existe gran variedad de títulos obligaciones y que la Ley de Sociedades Anónimas, en su artículo 291, obliga a recoger estas características en el título.

Las clases de obligaciones más importantes son:

A) Obligaciones simples u ordinarias: son aquéllas que se reembolsan en dinero.

B) Obligaciones convertibles: ofrecen al obligacionista la posibilidad de cambiar las obligaciones que posea por acciones de la empresa emisora de las mismas, de acuerdo con las reglas de conversión que se establezcan. Se define la relación de conversión como el cociente entre el precio de emisión de la obligación, que puede ser su valor nominal, y su precio de conversión, que no es más que el valor fijado para las acciones a los efectos de la conversión. También se define el valor de conversión, como el producto de la relación de conversión por la cotización actual de la acción, y la prima de conversión como la diferencia entre el precio de emisión y el valor de conversión.

Ejemplo: Obligaciones convertibles

C) Obligaciones con prima de reembolso o con lotes: las obligaciones con prima de reembolso, se reembolsan por encima del valor nominal y es precisamente la diferencia entre el valor de reembolso y el valor nominal lo que constituye la prima de reembolso.

Los lotes se refieren a cantidades de dinero que se entregan a las obligaciones cuando son amortizadas por sorteo.

D) Obligaciones indiciadas: el nominal a devolver, los intereses o ambos a la vez, se calculan en función de algún índice de referencia, por ejemplo: el índice de precios al consumo, índices financieros,bursátil, bancario, etc índices de precios basados en el valor de los metales preciosos, etc.

E) Obligaciones participativas: el tipo de interés de estas obligaciones consta de una parte fija y de otra variable, la cual está en función de los beneficios que obtenga la empresa, así pues, de alguna forma confieren la posibilidad de participar en los beneficios de la empresa emisora, lo cual hace atractivas a dichas obligaciones.

F) Obligaciones cupón cero: se denominan así por no recibir intereses a lo largo de la vida del título, si bien, su precio de emisión es bajo la par, es decir por debajo del valor nominal.

3.01.02 Valor teórico de una obligación

El valor teórico de una obligación será el valor actual del título, es decir la actualización de todos los flujos futuros que se recibirían por poseer dicho título, actualizados a la tasa de interés que desean ganar los inversores. El planteamiento expuesto es el realizado desde una óptica prospectiva, esto es, observando los flujos de dinero que quedan por delante del instante actual; también podríamos hallar el valor teórico de la obligación desde una óptica retrospectiva, observando los flujos de dinero anteriores al instante actual, y de esta forma el valor teórico se encontraría como la diferencia entre el valor capitalizado del precio de emisión y la capitalización de los flujos de dinero recibidos hasta el instante actual.

En este estudio usaremos la óptica prospectiva por ser, quizás, algo más sencilla. El enfoque que daremos en este apartado al valor teórico de la obligación, será el valor por el que el obligacionista estaría dispuesto a desprenderse de un título, que le garantiza el pago de unos intereses periódicos hasta su vencimiento y que en éste se le devuelve el nominal del título, por tanto supondremos, que el título no se amortiza anticipadamente antes de su vencimiento y que el valor por el que el obligacionista estaría dispuesto a desprenderse es el que matemáticamente le corresponda en ese instante.

Definamos las variables que formarán parte de las fórmulas empleadas en el cálculo del valor teórico:

Vs : valor teórico de la obligación en el instante "ts".

Vo : valor nominal de la obligación.

r : tasa de interés periódico.

ij : tasa de interés que desean ganar los obligacionistas en el período "j".

n : número de períodos desde el instante inicial hasta el vencimiento del título.

El planteamiento general del problema en cuestión podría representarse esquemáticamente:

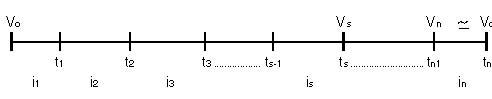
El valor teórico de la obligación sería:

$$V_{s}=\underbrace{\frac{V_{0}}{\left(1+i_{s+1}\right)}+\frac{V_{0\centerdot r}}{\left(1+i_{s+1}\right)\centerdot\left(1+i_{s+2}\right)}+\ldots\ldots+\frac{V_{0}\centerdot r}{\left(1+i_{s+1}\right)\centerdot\ldots\centerdot\left(1+i_{n}\right)}}$$

actualización del valor final de la obligación, que coincide con su valor nominal en el instante

$$+\underbrace{\frac{V_{0}\centerdot r}{\left(1+i_{s+1}\right)}+\frac{V_{0\centerdot r}}{\left(1+i_{s+1}\right)\centerdot\left(1+i_{s+2}\right)}+\ldots\ldots+\frac{V_{0}\centerdot r}{\left(1+i_{s+1}\right)\centerdot\ldots\centerdot\left(1+i_{n}\right)}} ;$$

actualización al instante "ts" de los intereses pagados en los instantes posteriores.

Esta expresión puede simplicarse notoriamente, si consideramos el caso más general en el que los intereses de los diversos períodos sean iguales, de esta forma obtendríamos la expresión:

$$V_{s} =\frac{V_{o}}{\left(1+i\right)^{\left(n-s\right)}} +\overset{n}{\underset{j=s+1}{\sum}} \frac{V_{o\centerdot r}}{\left(1+i\right)^{\left(j-s\right)}} =$$ $$=\frac{V_{o}}{\left(1+i\right)^{\left(n-s\right)}} +V_{o} \centerdot r\overset{n}{\underset{j=s+1}{\sum}} \frac{V_{0\centerdot r}}{\left(1+i\right)^{\left(j-s\right)}} =$$ $$ =\frac{V_{o}}{\left(1+i\right)^{\left(n-s\right)}} +V_{o} \centerdot r\left[\frac{1}{\left(1+i\right)}+\frac{1}{\left(1+i\right)^{2}}+\ldots\ldots+\frac{1}{\left(1+i\right)^{\left(n-s\right)}}\right]$$

El corchete representa una serie geométrica de razón:... $$\frac{1}{1+i}$$

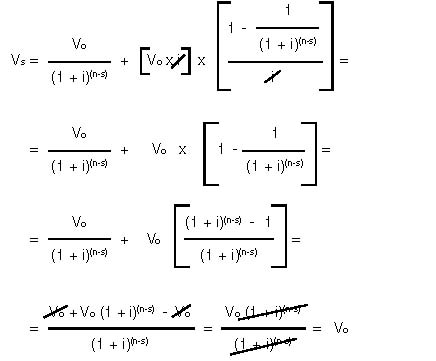
Primer término: $$a1=\frac{1}{1+i};$$y formada por (n-s) términos , cuya suma se calculará de acuerdo con lo especificado en la unidad anterior, resultando finalmente la expresión:

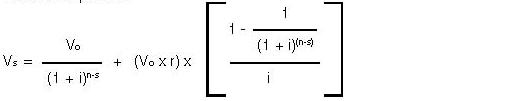
$$ V_{s=}\underbrace{\frac{V_{0}}{(1+i_{s+1})\centerdot(1+i_{s+2})\ldots\left(1+i_{n}\right)}} +\underbrace{\frac{V_{0}\centerdot r}{\left(1+i_{s}+1\right)}+\frac{V_{0}\centerdot r}{\left(1+i_{S}+1\right)\centerdot\left(1+i_{s}+2\right)}+\ldots+\frac{V_{0\centerdot}r}{\left(1+i_{s}+1\right)\centerdot\ldots\centerdot\left(1+i_{n}\right)}} ; $$

Esta expresión puede simplicarse notoriamente si consideramos el caso más general en el que los intereses de los diversos períodos sean iguales de esta forma obtendríamos la expresión:

$$V_{s} =\frac{V_{0}}{\left(1+i\right)^{\left(n-s\right)}} +^{n} \sum_{j=s+1} $$

De esta forma obtenemos que el valor teórico de la obligación en cualquier instante es el valor nominal del título, esto nos recuerda la amortización de préstamos tipo americano estudiado en la unidad anterior, en los cuales observábamos que el capital pendiente de amortizar en cualquier instante de la vida del préstamo era precisamente el capital inicial.

Como la obligación representa un préstamo que el obligacionista realiza al emisor del título, la cancelación de dicho préstamo es lo que el obligacionista recibiría por su título y correspondería al valor teórico de la obligación.

Por este motivo a este tipo de obligaciones se les denomina obligaciones tipo americano, que reciben unos intereses en determinados períodos y que al final de la vida del título reciben el nominal.

Ejemplo: Cálculo del valor teórico

Ejemplo: Cálculo de la tasa efectiva anual

3.01.03 Compra al descuento

Este caso correspondería a las obligaciones cupón cero, que las adquirimos a un precio inferior a su valor nominal, es decir, bajo la par, y no cobramos intereses a lo largo de la vida del título y al vencimiento nos reembolsan el nominal del título.

El planteamiento para conocer el valor del título en el instante de la compra, es el siguiente:

Vo=V x(1+i)t

donde las variables que intervienen significan

Vo : valor nominal del título.

V : valor de compra del título.

i : tasa de interés retributiva del título.

t : tiempo transcurrido desde la compra hasta el vencimiento.

Observamos que se usa la ley financiera de capitalización del interés compuesto.

Ejemplo: Cálculo del valor de compra