Módulo 2: SISTEMAS DE CÁLCULO DE COSTES
U.D. 5: El Direct Costing o sistema de Costes Parciales
Sección: 2
MathJax TeX Test Page
5.03
EL ANÁLISIS DEL COSTE-VOLUMEN-BENEFICIO
Visto en el apartado anterior el comportamiento
de los costes en el direct costing, vamos a superponer la gráfica
de los ingresos con la de los costes, para de esta forma obtener las zonas
en las que la empresa obtiene beneficios y en las que obtiene pérdidas.
El punto frontera entre la zona de beneficios y la zona de pérdidas
se llama punto de equilibrio, punto muerto o umbral de rentabilidad, y,
lógicamente, en este nivel de producción la empresa no obtiene
ni beneficios ni pérdidas, es decir, tiene un beneficio nulo.
En este apartado se mostrará la forma de calcular el punto de equilibrio,
tanto desde el punto de vista analítico como gráfico, pero
para ello deberemos establecer unas hipótesis, que conformarán
el análisis del coste-volumen-beneficio. Estas hipótesis
son las siguientes:
-
El comportamiento de los costes
variables y de los ingresos es lineal.
-
Los costes se compondrán
de los fijos y de los variables.
-
Los precios de venta son constantes.
-
Los costes variables unitarios
son constantes.
-
La productividad es la misma
para cualquier volumen de producción.
-
La composición de las
ventas será constante.
-
Los costes y los ingresos se
comparan respecto a las unidades producidas y vendidas.
A partir de estas hipótesis podemos calcular el punto de equilibrio
analítica y gráficamente.
Empecemos por el cálculo analítico:
Definimos como beneficio la diferencia entre los ingresos obtenidos por
la venta de unos productos y los costes que se han ocasionado para poderlos
vender.
Los costes de los productos vendidos serán la suma de los costes
variables y de los fijos. Los costes variables serán proporcionales
a las unidades fabricadas.
Por ello, la expresión de los costes de los productos fabricados
y vendidos será:
C = CV + CF = CVU
x q + CF
El significado de las variables que aparecen es:
C
=
costes totales
CV
=
costes variables totales
CF
=
costes fijos
CVU
=
coste variable unitario
q
=
unidades fabricadas y vendidas
El punto de equilibrio, punto muerto o umbral de rentabilidad lo obtendremos
haciendo nulo el beneficio, y de ahí deduciremos el número
de unidades fabricadas y vendidas; o simplemente vendidas, si no hay proceso
de fabricación por tratarse de una empresa comercial o de servicios:
B = 0 = I - C
I = C
Los ingresos de la venta “I” los podemos obtener como producto
del número de unidades vendidas “q”, por su precio de
venta “Pv”. Así, la expresión de los ingresos será:
I = Pv x q
Que, igualándola a la expresión obtenida para los costes,
nos permitirá despejar la cantidad de unidades que debemos vender
para obtener un beneficio nulo, “qe”.
Pv x qe = CVU
x qe + CF
(Pv - CVU)
x qe = CF
$$qe=\frac{CF}{PV-CVU}$$
Esta expresión nos da el número
mínimo de unidades que debemos vender para no obtener pérdidas
ni beneficios, es decir, para cubrir los costes de la empresa.
Otra expresión muy usual y práctica, derivada
de la anterior, es la que nos da el volumen de ventas que debemos
realizar para obtener un beneficio nulo. Para ello, multiplicaremos
ambos miembros de la expresión obtenida para el punto de equilibrio
por el precio de venta:
$$qe\centerdot Pv=\frac{CF\centerdot Pv}{PV-CVU}$$
El primer miembro de la ecuación nos da el volumen de ventas (ingresos por ventas)
que debemos realizar para obtener un beneficio nulo Y en el segundo
miembro, realizando unas sencillas operaciones algebraicas, como son
pasar el “Pv”, dividiendo, en el denominador, obtenemos la
expresión del volumen de ventas en el punto de equilibrio “Ve”.
$$Ve=\frac{CF}{PV-CVU}
=\frac{CF}{\frac{PV}{PV}-\frac{CVU}{PV}}$$
$$Ve=\frac{CF}{1-\frac{CVU}{PV}}$$
Observemos que el denominador de la
expresión del volumen de ventas en el punto de equilibrio nos da
el margen comercial en porcentaje sobre ventas, esto es: la cantidad que
obtenemos como diferencia entre los ingresos por venta y los costes variables
correspondientes, dividida por el volumen de ventas. Veámoslo:
$$margen\ comercial\ sobre\ ventas=\frac{ventas-costes\ variables}{ventas}
=1-\frac{costes\ variables}{ventas}
=1-\frac{CVU\centerdot q}{Pv\centerdot q}
=1-\frac{CVU}{PV}
$$
Otra expresión muy importante
para determinar el volumen de ventas es la que tiene en cuenta un determinado
beneficio establecido como un cierto porcentaje “b” sobre el
volumen de ventas. De este modo, los ingresos por ventas deberán
cubrir los costes fijos y variables de la empresa y, además, este
beneficio establecido de la forma comentada anteriormente. Expresándolo
matemáticamente, tendremos:
Pv x q = CVU
x q + CF + b x Pv x q
(Pv - CVU
- b x Pv) x q = CF
$$q=\frac{CF}{Pv-CVU-b\centerdot Pv}$$
$$q\centerdot Pv=\frac{CF\centerdot Pv}{Pv-CVU-b\centerdot Pv}$$
$$Vb=\frac{CF}{\frac{Pv-CVU-b\centerdot Pv}{Pv}}
=\frac{CF}{1-\frac{CVu}{Pv}-b}
=\frac{CF}{1-\left(\frac{CVu}{Pv}+b\right)}
$$$$Vb
=\frac{CF}{1-\left(\frac{CVu}{Pv}+b\right)}
$$
Esta expresión nos da el volumen
de ventas “Vb”, que cubre no sólo los costes, sino que
además nos garantiza un cierto beneficio establecido como un cierto
porcentaje “b” del volumen de ventas. También podríamos
interpretar el denominador de la expresión anterior como un margen
comercial modificado por el coeficiente “b”, que nos remite
al beneficio exigido, de forma que este margen comercial será menor
que el obtenido en la expresión del volumen de ventas “Ve”
para el punto de equilibrio, y, por consiguiente, el volumen de ventas
“Vb” será mayor que el “Ve”.
Por último, vamos a representar gráficamente los ingresos
y los costes en función de las unidades vendidas, y, seguidamente,
superpondremos estos gráficos para obtener el gráfico que
nos mostrará el punto de equilibrio y las zonas de beneficio y
de pérdidas para la empresa.
Superponiendo los gráficos anteriores
obtenemos:
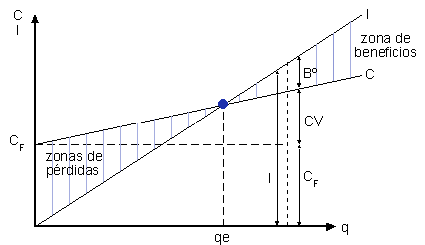
Geométricamente, vemos como
el punto de equilibrio “qe” se encuentra en la intersección
de las rectas de ingresos y de costes. En dicho punto, los ingresos y los
costes coinciden en valor, y, por lo tanto, el beneficio es nulo.
El conocimiento de este gráfico es muy importante, ya que podemos
obtener de forma cualitativa los efectos que tendría, sobre el
punto de equilibrio, cualquier modificación en los precios o
en los costes, ya sea en los fijos o en los variables.
Ya hemos comentado anteriormente que
el precio de venta era la pendiente de la recta de ingresos. Por lo tanto,
un aumento de los precios de venta aumentaría la pendiente de la
recta de ingresos, lo cual disminuiría el número de unidades
a vender para lograr beneficio nulo, considerando inalterados los costes.
En el caso de disminución de los precios de venta sucedería
lo contrario, es decir, disminuiría la pendiente de la recta de
ingresos y aumentaría el número de unidades a vender para
alcanzar el punto de equilibrio.
Representemos gráficamente el primer caso:
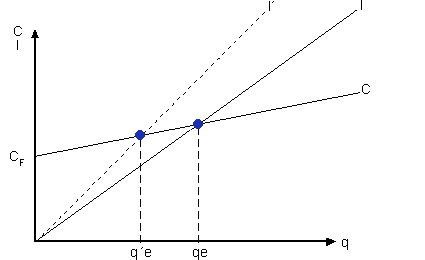
“I´” es la nueva recta
de ingresos con precios de venta “Pv”, más altos.
“q´e” sería el nuevo punto de equilibrio.
Este caso puede darse, por ejemplo,
cuando hay un encarecimiento de la materia prima, y el mercado no nos
permite elevar los precios de venta. En esta situación la pendiente
de la recta de costes, que es el coste variable unitario, se elevará
al elevarse el coste variable unitario y, en consecuencia, aumentará
el número de unidades a vender para lograr el beneficio nulo. En
otro caso, si el coste variable unitario disminuyera sucedería lo
contrario a lo expuesto. Al no variar el precio de venta, la recta de
ingresos no se alterará, y si suponemos que los costes fijos permanecen
invariables, la representación gráfica de lo expuesto sería:
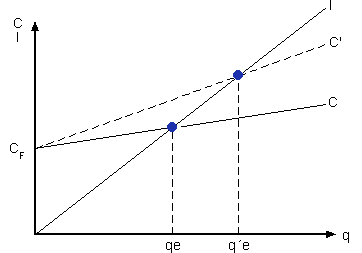
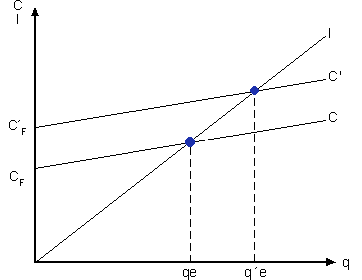
“C'” es la nueva recta de
costes que, manteniendo los costes fijos, representa un aumento de los variables. Con esta
nueva situación, el punto de equilibrio es “q´e”.
Si solamente varían los costes
fijos, permaneciendo constantes el resto de las variables, las pendientes
de las rectas de costes y de ingresos no variarán. Por lo tanto,
el efecto que supondrá un aumento de los costes fijos será
un desplazamiento paralelo de la recta de costes hacia arriba, mientras
que si estos disminuyen el desplazamiento paralelo de la recta de costes
será hacia abajo. Las consecuencias de ello serían que, en
el primer caso, aumento de los costes fijos, aumentará el número
de unidades a vender para lograr el punto de equilibrio, mientras que
en el segundo caso disminuirá el número de unidades a vender
para obtener dicho punto. Veamos gráficamente la representación
del aumento de los costes fijos:
Ver caso práctico: Análisis de coste-volumen-beneficio-servicios
Ver caso práctico: Análisis de coste-volumen-beneficio-producción
5.04
EL MéTODO DEL DIRECT
COSTING
El método del direct
costing se basa en incorporar al coste del producto los costes variables,
enfrentando éstos a los ingresos por venta y hallando el margen comercial
como diferencia entre éstos y los costes variables.
Al margen comercial se le restarán
los costes fijos para obtener así el resultado de explotación.
Si bien ya hemos comentado que existe una variante de este método,
que asigna a los productos parte de los costes fijos, obteniendo entonces
el margen de contribución como diferencia entre el margen comercial
y los costes fijos asignables.
Por último, restando al margen
de contribución los costes fijos no asignables obtendremos el resultado
de explotación.
La diferencia fundamental con el full
costing es que en el direct costing sólo se asignan a las secciones
los costes variables de fabricación, y con estos se opera igual
que en el full costing, esto es realizando el reparto primario, después
el secundario, si procede, y, por último, se imputan a los productos
en función de unidades de obra. Con ello obtendremos el coste industrial
de las ventas y el resto de costes variables, los comerciales y de administración
que proceda para así poder determinar el margen comercial. Si optamos
por la variante de este método que asigna a los productos parte
de los costes fijos, estos serán tratados de la misma forma que
en el full costing. El resto de costes fijos, los no asignables a los
productos, irán directamente al resultado del período.
Es evidente que en el direct costing
aparecerán diferentes valoraciones en los inventarios, y, en consecuencia, se obtendrán
distintos resultados que en el full costing, y ello es debido al tratamiento
que el direct costing da a los costes fijos.
A continuación, desarrollemos
un caso práctico que nos aclare lo expuesto.
Ver caso práctico:
El método del Direct Costing-servicios
Ver caso práctico:
El método del Direct Costing-producción